Multiscale Control Concepts for Transport-Dominated Problems
Description
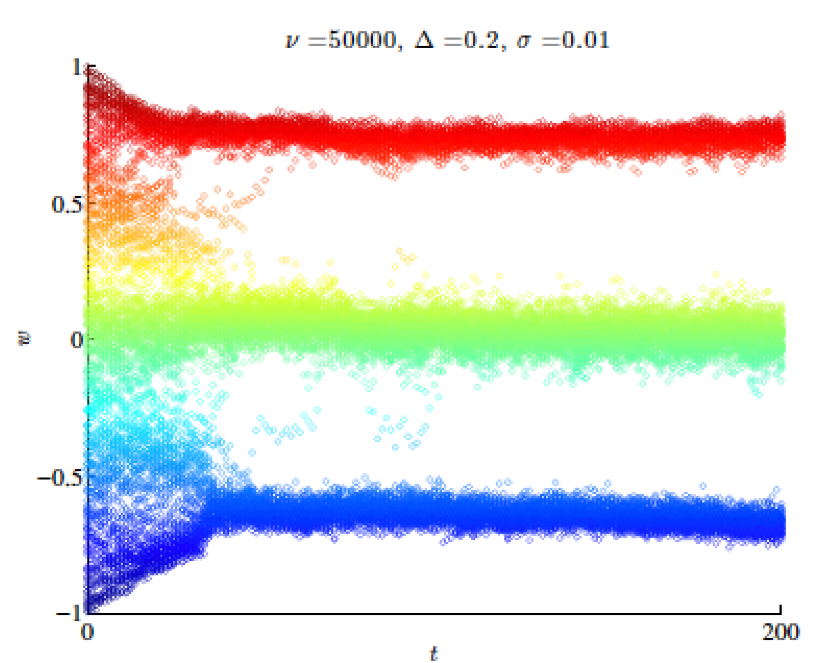
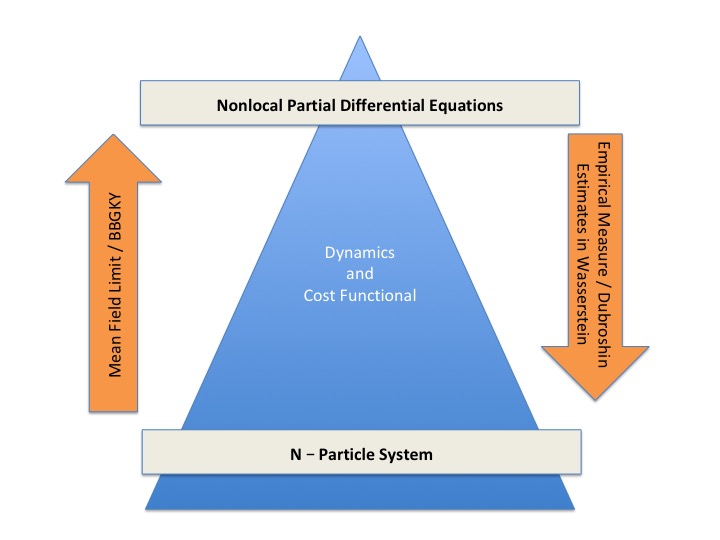
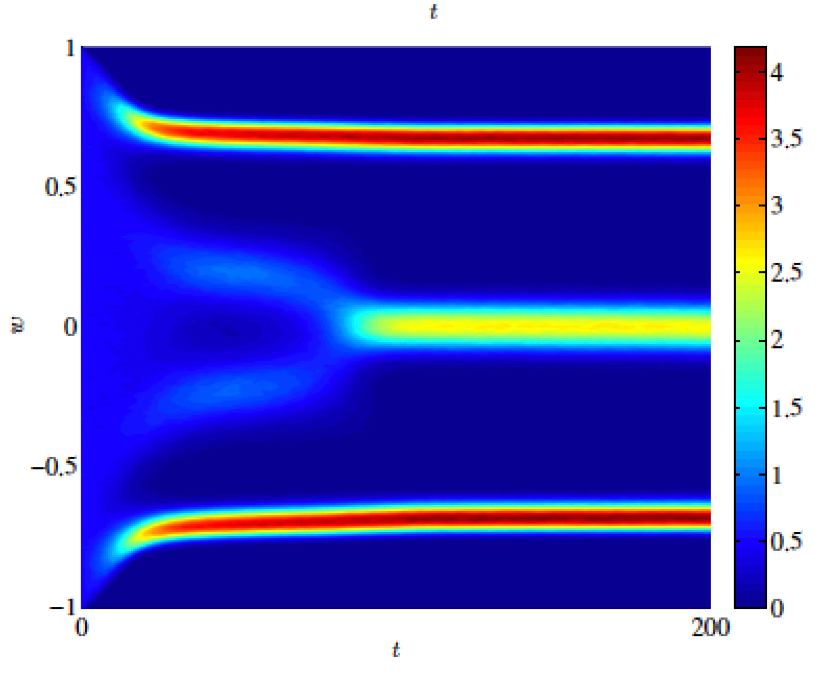
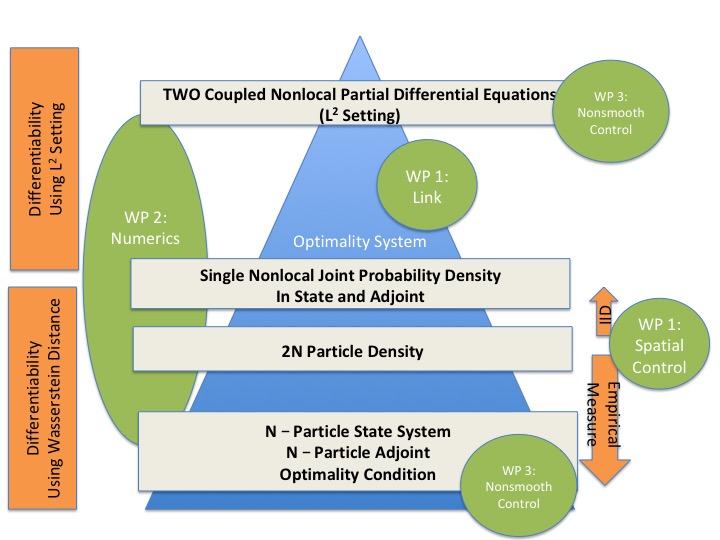
Publications
Anna Thünen, Sven Leyffer, Sebastian Sager: State Elimination for Mixed-Integer Optimal Control of Partial Differential Equations by Semigroup Theory, Optim Control Appl Meth., 2022.
Preprints
Michael Herty, Stefan Ulbrich: Numerics and Control of Conservation Laws (SPP1962-199, 10/2022, [bib])
Michael Herty, Sonja Steffensen, Anna Thünen: Multiscale Control of Stackelberg Games (SPP1962-150, 11/2020, [bib])
Simone Göttlich, Michael Herty, Gediyon Weldegiyorgis: Input-to-State Stability of a Scalar Conservation Law with Nonlocal Velocity (SPP1962-149, 11/2020, [bib])
Martin Frank, Michael Herty, Torsten Trimborn: Microscopic Derivation of Mean Field Game Models (SPP1962-126, 11/2019, [bib])
Research Area
Modeling, problem analysis, algorithm design and convergence analysis
The focus of this area is on the development and analysis of genuinely non-smooth models in the sciences in order to properly capture real-world effects and to avoid comprising smoothing approaches. In simulation and optimization this requires to advance set-valued analysis and the design of robust algorithms for non-smooth problems.Realization of algorithms, adaptive discretization and model reduction
As the target applications of this SPP involve non-smooth structures and partial differential operators, the discretization of the associated problems and robust error estimation are important issues to be address, and proper model-reduction techniques need to be developed.Members
Project Related News
-
Oct 31, 2022 : New preprint submitted
Stefan Ulbrich submitted the preprint SPP1962-199 Numerics and Control of Conservation Laws.
-
Nov 06, 2020 : New preprint submitted
Anna Thünen submitted the preprint SPP1962-150 Multiscale Control of Stackelberg Games.
-
Nov 05, 2020 : New preprint submitted
Anna Thünen submitted the preprint SPP1962-149 Input-to-State Stability of a Scalar Conservation Law with Nonlocal Velocity.
-
Nov 04, 2019 : New preprint submitted
Anna Thünen submitted the preprint SPP1962-126 Microscopic Derivation of Mean Field Game Models.

